Az érintőleges a grafikon az egyenlet az érintő funkciók
Tekintsük a következő kép:
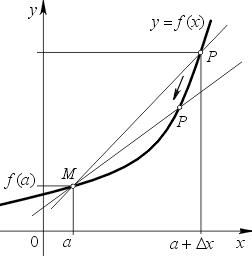
Ez ábrázolja egy függvény az y = f (x), differenciálható a ponton a. Jelzett az M pont koordinátái (a, f (a)). Keresztül egy tetszőleges P pont (a + Ax; f (a + Ax)) generált hajtjuk szekáns MR.
Ha most a P pont a shift menetrend az M pont, majd a sort LL fog forogni ezen a ponton M. Amikor Ah fog általában nulla. Ebből tudjuk megfogalmazni meghatározását érintő a függvény grafikonját.
Az érintő a függvény grafikonját
Az érintő a függvény grafikonját van egy határ helyzetét a keresztmetszet nullához növekmény az érvelés. Meg kell érteni, hogy a létezése a származék f x0 azt jelenti, hogy ezen a ponton a gráfnak egy érintő hozzá.
A szögletes együtthatója tangense egyenlő a függvény deriváltját ponton f „(x0). Ez a geometriai jelentése a-származék. Az érintő a grafikon a ponton x0 differenciálható függvények f - egy vonal ponton áthaladó (x0, f (x0)), és amelynek van egy szögletes együtthatót f „(x0).
Az egyenlet az érintő
Próbáljuk meg megszerezni az egyenlet érintő a grafikon f pontnál (x0, f (x0)). vonal egyenlete meredekség k jelentése a következő:
Mivel van egy meredeksége egyenlő a származékot f „(x0). Az egyenlet a következő alakú: y = f „(x0) * x + b.
Most az A értékét b. Ehhez használja a tény, hogy a függvény átmegy a ponton A.
f (x0) = f '(x0) * X0 + b, b és így kifejezni kapjunk b = f (x0) - f' (x0) * x0.
Helyettesítsük a kapott érték az egyenletben az érintő:
y = f '(x0) * x + b = F' (x0) * x + f (x0) - f '(x0) * x0 = f (x0) + f' (x0) * (x - x0).
y = f (x0) + f „(x0) * (x - x0).
Tekintsük a következő példát: megtalálják az egyenlet az érintő a grafikon a f (x) = x 3 - 2 * x 2 + 1 x = 2.
2. f (x0) = f (2) = 2 2 - 2 * 2 2 + 1 = 1.
3. f „(x) = 3 * x 2 - 4 * X.
4. F '(x0) = f' (2) = 3 * 2 2 - 4 * 2 = 4.
5. Behelyettesítve a kapott értékeket a képlet az érintő, kapjuk: y = 1 + 4 * (x - 2). Bővítése konzolok és hivatkozva hasonló kifejezések azt kapjuk: y = 4 * x - 7.
Az általános rendszer a készítmény az egyenlet az érintő a grafikon y = f (x):
1. Határozza meg x0.
2. Számítsuk ki f (x0).
3. Számítsuk ki f „(x)
4. Számítsuk f „(x0)
5. Behelyettesítve az értékeket az egyenletbe az érintő y = f (x0) + f „(x0) * (x - x0).